1. Estimating Total FLOPs

We only consider the FLOPs of Transformer layers, excluding the embedding layer and the output layer.

  • Attention:

    1. Each projection for Q, K and V is matmul of input (B, S, H) and weight (H, H), yielding (B, S, H):
      $$ \text{FLOPs} = 3 \times (2 \times B \times S \times H \times H) = 6 \times B \times S \times H^2 $$
    2. $S = QK^T$, matmul of $Q$ (B, S, H) and $K^T$ (B, H, S), yielding (B, S, S):
      $$ \text{FLOPs} = 2 \times B \times S \times S \times H = 2 \times B \times S^2 \times H $$
    3. $L = S \cdot V$, matmul of $S$ (B, S, S) and $V$ (B, S, H), yielding (B, S, H):
      $$ \text{FLOPs} = 2 \times B \times S \times H \times S $$
    4. $O = L \cdot W_O$, matmul of $L$ (B, S, H) and $W_O$ (H, H), yielding (B, S, H):
      $$ \text{FLOPs} = 2 \times B \times S \times H^2 $$
    5. Total attention FLOPs per Transformer layer: $$ \text{FLOPs} = 8 \times B \times S \times H^2 + 4 \times B \times S^2 \times H $$

  • Feed-Forward Networek
    Typically 2 linear layers, one mapping (B, S, H) to (B, S, 4H) and the other mapping (B, S, 4H) to (B, S, H):

    • Total FFN FLOPs per Transformer layer:

      $$ \begin{align*} \text{FLOPs} &= 2 \times B \times S \times H \times (4 \times H) + 2 \times B \times S \times (4 \times H) \times H \\ &= 16 \times B \times S \times H^2 \end{align*} $$

  • Total FLOPs: $N$ Layers of Transformer
    Each Transformer layer consists of an attention mechanism and a feed-forward network

    • When prefilling, the total FLOPs is:

      $$ \text{FLOPs}_\text{total} = N (24 B S H^2 + 4 B S^2 H) $$

    • When decoding, suppose the input is of shape (B, Si, H) and KV cache is of shape (B, Sc, H), the total FLOPs is:

      $$ \text{FLOPs}_\text{total} = N (24 B S_i H^2 + 4 B S_i S_c H) $$

2. Estimating Total Bytes Transfered

In FP16, each parameter or activation element is 2 bytes.

Data transferred includes loading model weights and handling activations.

Suppose we have a $Z$-B-fp16 model and $N$ Transformer layers, each with input size (B, S, H).

  • Model Weights
    A $Z$-B-fp16 model has $Z \times 10^9$ fp16 parameters, each 2 bytes:

    $$ \text{Bytes}_\text{weights} = Z \times 10^9 \times 2 ~ \text{Bytes} = 2 \times Z ~ \text{GBytes} $$

    In an optimized GPU inference, weights are typically loaded into high-bandwidth memory (HBM) once and reused, so we assume $2Z$ GB is read once per forward pass.

  • Activations

    • For each Transfomer layer, input and output activations are of shape (B, S, H), and each element is 2 bytes in fp16: $$ \text{Bytes}_\text{act-layer} = B \times S \times H \times 2 ~ \text{Bytes} $$
    • For $N$ layers, activations are computed sequentially. Since each layer’s output becomes the next layer’s input (read once, written once):
      $$ \begin{align*} \text{Bytes}_\text{act-total} &= 2 \times N \times \text{Bytes}_\text{act-layer} ~ \text{Bytes} \\ &= 4 \times N \times B \times S \times H ~ \text{Bytes} \end{align*} $$

  • KV Caches
    When decoding, each Transformer layer would load cached K and V both of shape (B, Sc, H). After decoding, the new K and V of shape (B, Si, H) are computed and cached for the next layer. So the bytes transfered for one forward pass is:

    $$ \text{Bytes}_\text{KV} = N \times (B \times S_c \times H + 2 \times B \times S_i \times H) \times 2 ~ \text{Bytes} $$

  • Total Data Transferred

    • When prefilling, the total bytes transferred is:

      $$ \begin{align*} \text{Bytes}_\text{total} &= \text{Bytes}_\text{weights} + \text{Bytes}_\text{act-total} \\ &= 2 Z \text{e}^9 + 4 N B S H ~ \text{Bytes} \end{align*} $$

    • When decoding, suppose cached sequence length is $S_c$ and the input sequence length is $S_i$, the total bytes transferred is:

      $$ \begin{align*} \text{Bytes}_\text{total} &= \text{Bytes}_\text{weights} + \text{Bytes}_\text{act-total} + \text{Bytes}_\text{KV} \\ &= 2 Z \text{e}^{9} + 8 N B S_i H + 2 N B S_c H ~ \text{Bytes} \end{align*} $$

3. Arithmetic Intensity

When prefilling, there is no cached K and V, so the arithmetic intensity is:

$$ \begin{align*} \text{Arithmetic Intensity} &= \text{FLOPs}_\text{total} / \text{Bytes}_\text{total} \\ &= \frac{N (24 B S H^2 + 4 B S^2 H)}{2 Z 10^9 + 4 N B S H} \end{align*} $$

When decoding, suppose cached sequence length is $S_c$ and the input sequence length is $S_i$ , then the arithmetic intensity is:

$$ \begin{align*} \text{Arithmetic Intensity} &= \text{FLOPs}_\text{total} / \text{Bytes}_\text{total} \\ &= \frac{N (24 B S_i H^2 + 4 B S_i S_c H)}{2 Z 10^9 + 8 N B S_i H + 2 N B S_c H} \end{align*} $$

4. Roofline Model

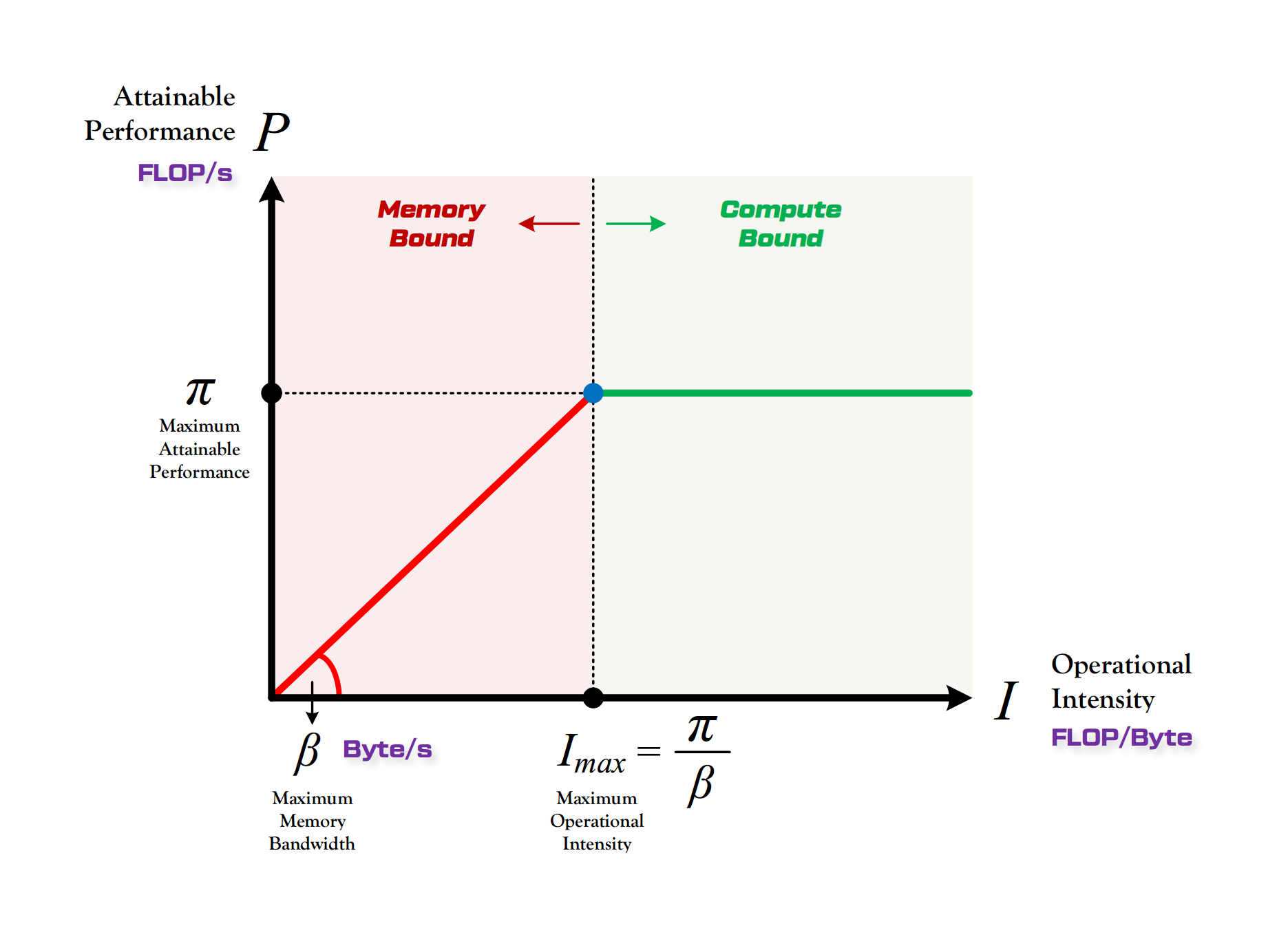
Roofline Model. If the arithmetic intensity is on the right side of the machine balance, the performance compute-bound. If it is on the left side, the performance is memory-bound.

A100-80GB has the following hardware `specifications:

  • Peak FLOPs ($\pi$): $312 \times 10^{12}$ FLOPs/s
  • Memory Bandwidth ($\beta$): $2039 \times 10^9$ B/s
  • Machine Balance ($I_{max}$): $312 \times 10^{12} / (2039 \times 10^9) \approx 153$ FLOPs/Byte

Here are two examples of arithmetic intensity estimation:

5. Discussion: Tensor Parallelism

If the model is split across multiple GPUs using TP, the hidden size H and the model weight is divided by the number of GPUs.