Dive into Paged Attention

1. Why Attention’s $O_i$ only depends on $Q_i$

The Attention formula is:

$$ O=Attention(Q,K,V)=softmax\left(\frac{QK^T}{\sqrt{d_k}}\right)V $$

Assume $Q=\begin{bmatrix}Q_0\\Q_1\end{bmatrix}$, $K=\begin{bmatrix}K_0\\K_1\end{bmatrix}$

Then:

$$ O=softmax(\frac{\begin{bmatrix}Q_0K_0^T&Q_0K_1^T\\Q_1K_0^T&Q_1K_1^T\end{bmatrix}}{\sqrt{d_k}})V $$

Let:

$$ A=\begin{bmatrix}A_0\\A_1\end{bmatrix}=\begin{bmatrix}Q_0K_0^T&Q_0K_1^T\\Q_1K_0^T&Q_1K_1^T\end{bmatrix},f(x)=\frac{softmax(x)}{\sqrt{d_k}} $$

At this point, $A_1$ only depends on $Q_1$ and is independent of $Q_0$, so:

$$ \begin{bmatrix}O_0\\O_1\end{bmatrix}=O=\begin{bmatrix}f(A_0)\\f(A_1)\end{bmatrix}V=\begin{bmatrix}f(A_0)V\\f(A_1)V\end{bmatrix} $$

Therefore, $O_i$ only depends on $A_i$, and according to the definition of $A$, $A_i$ only depends on $Q_i$, meaning:

The $i$-th output of the Attention matrix only depends on the $i$-th $Q$ and is independent of previous $Q$s.

Summary:

When predicting the next token, we only need to calculate the corresponding Q_new for the new token and perform attention calculation with the previously cached K_cache and V_cache.
The new K_new and V_new will be added to the cache to provide the foundation for the next token generation.
This process avoids repeated calculations for all historical tokens, greatly improving efficiency.

2. KV Cache Incremental Process

Example code:

“Learning-Programming-Massively-Parallel-Processors/src/pmpp/models/attention.py”

2.1. Prefilling: Initial Input (Complete Sequence) Calculation

For the initial input sequence (seq_len, vocab_size), we obtain Q, K, and V through linear transformations, all with shape (seq_len, embed_dim) (see this).
Using Q and K to calculate attention scores through dot product, then combining with V to compute the output (seq_len, embed_dim) (see this), this is the first complete calculation for the initial sequence.

2.2. Decoding: Incremental Calculation When Predicting Next Token:

When predicting the next token, there’s no need to perform complete Q, K, V calculations for the entire sequence. Instead, only an incremental calculation for the newly generated token is required. The process is as follows:

Input New Token: Take the generated token from last round as input sequence, obtain Q_new, K_new and V_new through linear transformation.
Update KV Cache: K_new and V_new are added to the end of K_cache and V_cache, making them a pair of (kv_len + 1, embed_dim) vectors.
Attention Calculation with Updated K_cache and V_cache: Use Q_new to perform attention calculation with updated K_cache and V_cache. Q_new can directly perform dot product with K_cache to get attention scores, then combine with V_cache to get new output.
Output: The output after attention calculation has shape (1, embed_dim), which is the newly generated token.

3. Paged Attention in vllm

3.1. Motivation: Memory Wastes

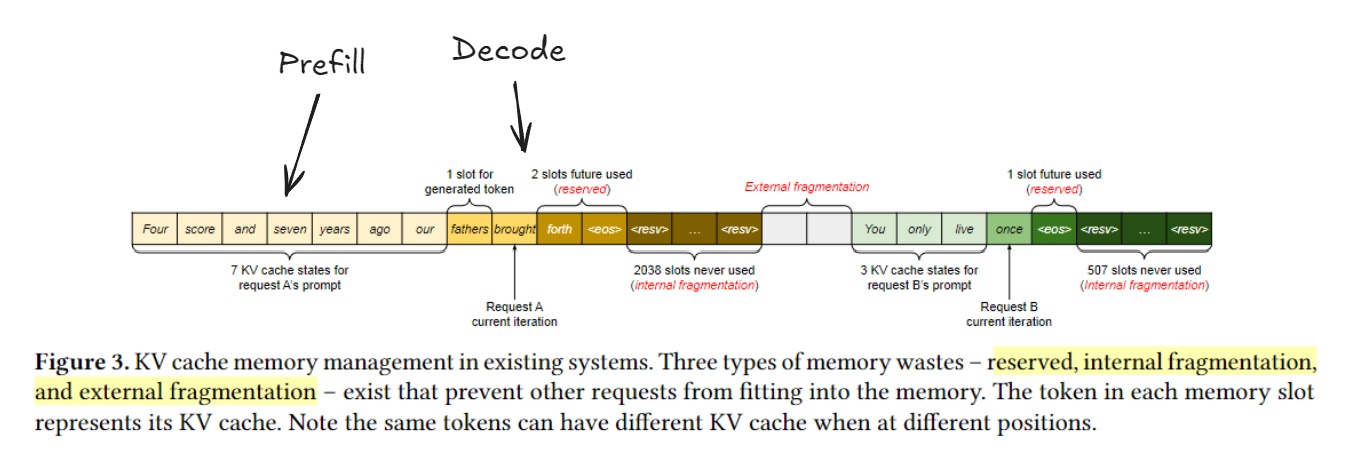
The above figure shows possible memory waste scenarios. The main issue is that we don’t know where the EOS (end of sequence) token is. Random memory allocation may lead to significant memory fragmentation, resulting in reduced throughput.

3.2. Solution: Managing Caches with Pages

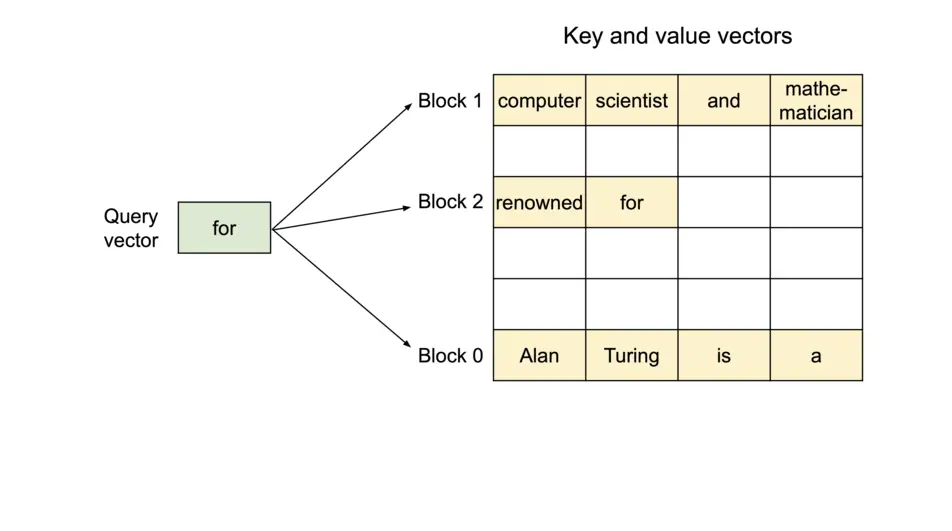
The above figure demonstrates how vLLM manages memory using Paged Attention.

In simple terms, before inference begins, vLLM allocates two long Tensors (k_cache and v_cache) for each Decoder Layer, dividing these Tensors into continuous equal-length PA blocks (each row in the figure represents one PA Block). Each PA Block can store K or V cache for BLOCK_SIZE tokens (each token’s shape can be recognized as (num_heads, head_size)).

Therefore, the shapes of k_cache and v_cache can be recognized as (num_blocks, block_size, num_heads, head_size).

For a continuous sequence, PA blocks are allocated before the prefilling stage, and during inference:

When computing prompt attention, the input K and V are first stored in k_cache and v_cache according to PA blocks; then attention is calculated using the entire QKV.
When computing new tokens, Q and the block table are used to calculate attention during the decode phase; at this point, the memory access is to the PA blocks in k_cache and v_cache.

5. Paged Attention Kernel in Details

References:
vLLM Paged Attention
vLLM皇冠上的明珠：深入浅出理解PagedAttention CUDA实现

The general structure of the Paged Attention kernel is as follows:

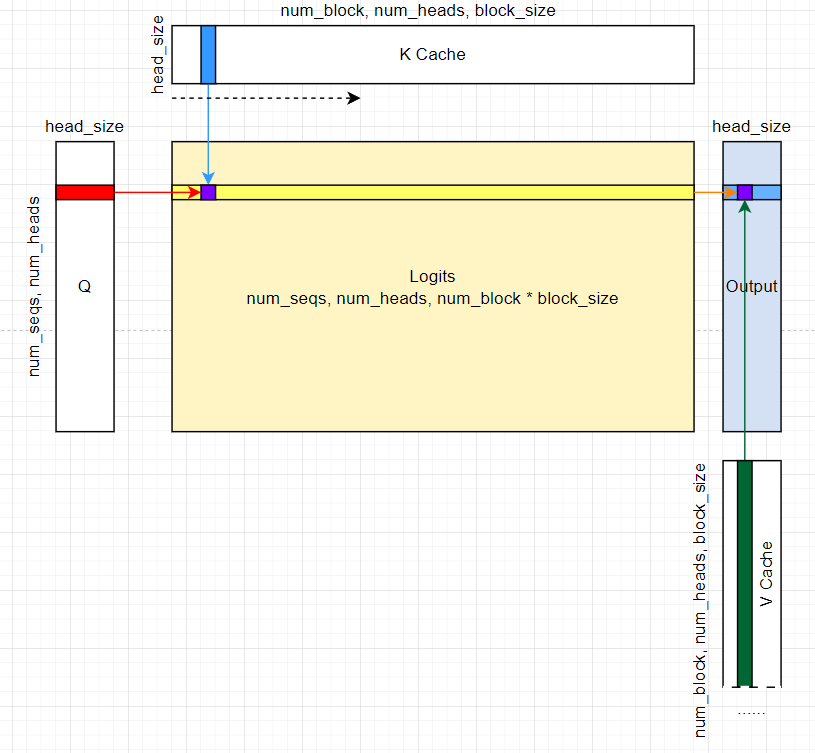
5.1. 输入输出输出分析和参数说明

// Grid: (num_heads, num_seqs, 1).
template<
typename scalar_t,
int HEAD_SIZE,
int BLOCK_SIZE,
int NUM_THREADS,
int PARTITION_SIZE = 0>
__device__ void paged_attention_kernel(
... // Other side args.
const scalar_t* __restrict__ out,       // [num_seqs, num_heads, max_num_partitions, head_size]
const scalar_t* __restrict__ q,         // [num_seqs, num_heads, head_size]
const scalar_t* __restrict__ k_cache,   // [num_blocks, num_kv_heads, head_size/x, block_size, x]
const scalar_t* __restrict__ v_cache,   // [num_blocks, num_kv_heads, head_size, block_size]
... // Other side args.
)

模板参数说明:

scalar_t 元素类型 (实际代码中还有 cache_t 表示 KV cache 的元素类型).
HEAD_SIZE 每个 head 中元素数量.
BLOCK_SIZE 每个 PA block 中的 token 数量.
1. KV cache 被存储在不同 PA blocks. 每个 PA block 存储一个 head 中 BLOCK_SIZE 个 token.
  例如, 若 BLOCK_SIZE=16, HEAD_SIZE=128, 则一个 PA block 能存储一个 head 的 16 * 128 = 2048 个元素.
2. 每个 PA block 可能只包含一部分的 context tokens.
3. 从 page 角度看, KV cache 是若干个 page 的集合;
NUM_THREADS 每个 CUDA thread block 中 thread 的数量.
PARTITION_SIZE 参与 TP 的 GPU 数量, 默认 0 表示单卡. (以下都以单卡为例说明)

额外的一些参数:

num_seqs: 本次推理请求 sequence 数目.
由于这个 kernel 只处理 decode 阶段单 query attention, 所以实际上每个 sequence 只有一个 query token.
num_heads: Q 的 head 数目
num_kv_heads: KV 的 head 数目, 对于 MHA 其值和 num_heads 相同; 如果是 GQA, MQA 则 num_kv_heads 小于 num_head.
head_size: 即 HEAD_SIZE
k_cache: (num_blocks, num_kv_heads, head_size/x, block_size, x), 其中 x 表示 THREAD_GROUP_SIZE * VEC_SIZE 的大小 (后面会细说).

下面结合 GPU architecture 初步分析一下参数.

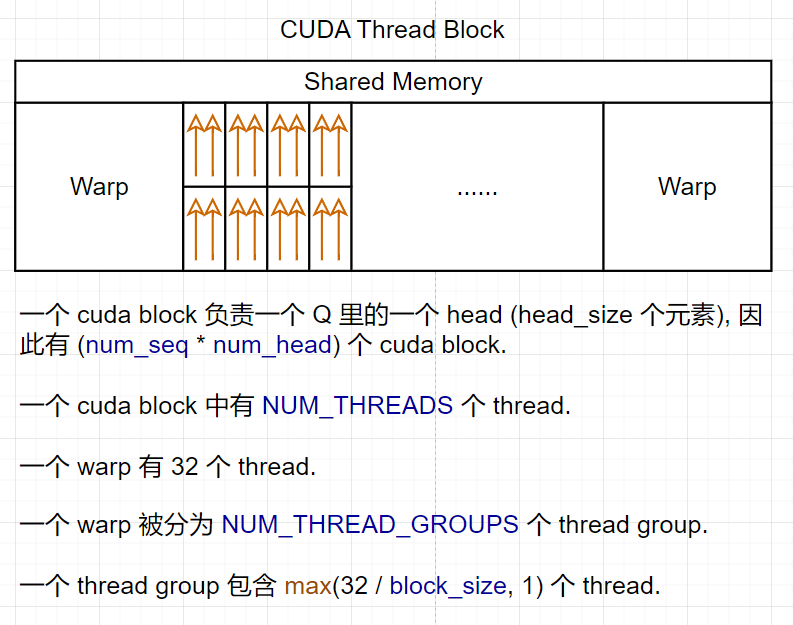
🧐 为什么要分 thread group?

因为当一个 cuda block 要取的数据比较少的时候 (计算 QK), 一个 thread group 分别一次取 Q 和 K 中 16B; 当一个 cuda block 要取的数据比较多的时候 (计算 LV), 一个 thread 取 16B.

5.2.Shared Memory: `q_vecs` 的写入

从 kernel 中的第一个申请的 shared memory 开始说.

关于 shared memeory:
在 kernel 中申请的 shared memory 被当前 cuda block 中的所有 thread 共享.
shared memory 的作用是为了减少 global memory 的访问次数，提高访存效率.

以下代码申请了一块 shared memroy 被整个 CUDA Block 中所有 kernel 共享:

__shared__ Q_vec q_vecs[THREAD_GROUP_SIZE][NUM_VECS_PER_THREAD];

首先, q_vecs 覆盖了 Q 中 head_size 个元素 - 这也是一个 cuda block 需要处理的数据量.

接着再说两个维度的参数的意思:

constexpr int NUM_ELEMS_PER_THREAD = HEAD_SIZE / THREAD_GROUP_SIZE;
constexpr int NUM_VECS_PER_THREAD = NUM_ELEMS_PER_THREAD / VEC_SIZE;

THREAD_GROUP_SIZE: 每个 thread group 中的 thread 数量. 注意, 一个 cuda block 中有 NUM_THREADS 个 thread, NUM_THREAD_GROUPS 个 thread group. THREAD_GROUP_SIZE = MAX(WARP_SIZE/BLOCK_SIZE, 1).
NUM_VECS_PER_THREAD: HEAD_SIZE 能被分成多少个 16B. (这个变量这么命名的理由是后面读取 K 的时候每个 thread 会往自己的寄存器内读 NUM_VECS_PER_THREAD 个 k_vec.)

证明: q_vecs 覆盖 Q 的一个 head, 并且 NUM_VECS_PER_THREAD 表示 Q 的一个 head 被分成多少个 16B.
=> THREAD_GROUP_SIZE * VEC_SIZE = 16B / sizeof(scalar_t);
=> NUM_VECS_PER_THREAD * 16B / sizeof(scalar_t) = HEAD_SIZE;

然后看 load Q 的代码, 建议结合下面的图一起看:

  // Load Q to shmem
#pragma unroll
for (int i = thread_group_idx; i < NUM_VECS_PER_THREAD;
        i += NUM_THREAD_GROUPS) {
    const int vec_idx = thread_group_offset + i * THREAD_GROUP_SIZE;
    q_vecs[thread_group_offset][i] =
        *reinterpret_cast<const Q_vec*>(q_ptr + vec_idx * VEC_SIZE);
}

thread_group_idx 表示当前 thread 属于当前 cuda block 中第几个 thread group.
thread_group_offset 表示当前 thread 在当前 thread group 中是第几个 thread.

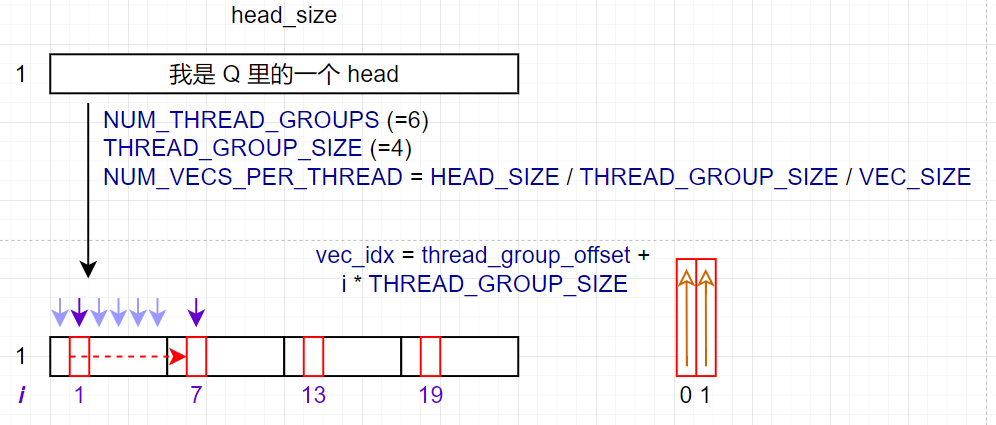
上图展示了循环具体是怎么跑的.

一个紫色箭头表示一个 thread group.
NUM_VECS_PER_THREAD 表示 HEAD_SIZE 能被分成多少个 16B.
实际读取 Q 的内存时, 所有 thread group 从 Q 的起始位置紧密排列, 根据图上看的话一共有 NUM_THREAD_GROUPS 个紫色箭头.
所有 thread group 读取一次 Q 并存入 q_vecs 对应循环中的一次迭代; 因此下次迭代 thread group 需要向后偏移 NUM_THREAD_GROUPS 个位置 (例如 i 从 1 变为 7).
此外, 读一次 16B 对应一个 thread 来说自然也是取一个 VEC.
对应到 kernel 编写, 还需要计算当前 thread 具体读取哪个 vec; 因此得到 vec_idx = thread_group_offset + i * THREAD_GROUP_SIZE.

🤔 这里会不会有 bank conflict?

总之现在我们把 (1, head_size) 大小的元素读到了 cuda block 共享的 shared memory q_vecs 中.

5.3. 读取 K Cache 并计算 QK

现在从 cuda block 的角度看, 当前 block 已经获得了自己要算的 Q 中的一个 head (形状为 (1, head_size)), 接下来就是计算 Q 和 K 的点积.

点积过程是把当前 block 拥有的 Q head 和整个 K Cache (迭代地) 进行点积运算. 参考下图:

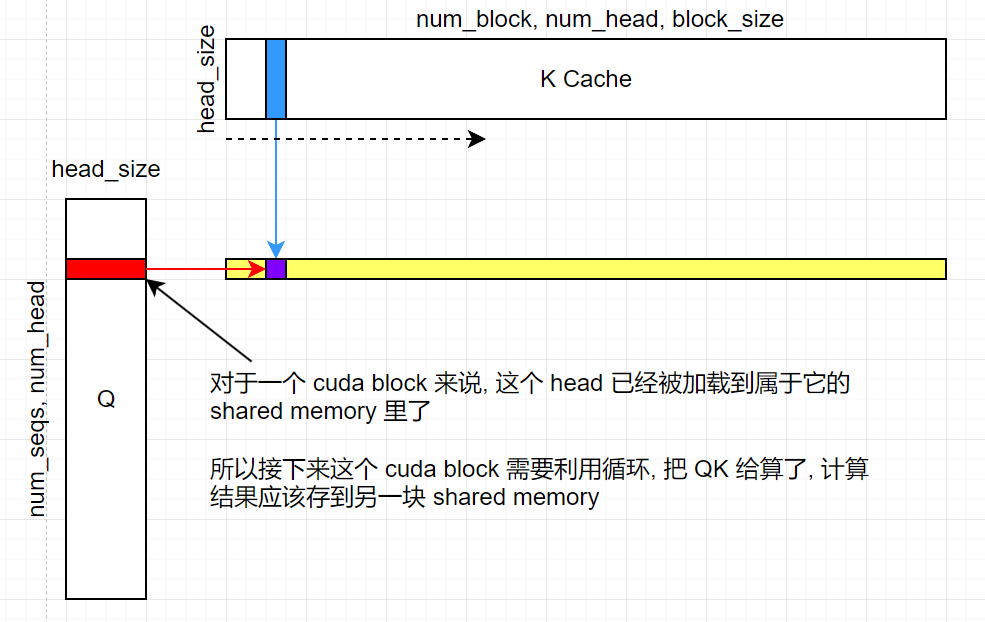
QK 乘积实际上被暂存在 logits (也是一块 shared memory) 中, 之后会被用来计算 softmax.

😇 看下循环的具体代码吧:

// Loop 1
for (int block_idx = start_block_idx + warp_idx; block_idx < end_block_idx;
        block_idx += NUM_WARPS) {
    // Physical block calculation ...
    // Loop 2
    for (int i = 0; i < NUM_TOKENS_PER_THREAD_GROUP; i++) {
        // Offset calculation ...
        K_vec k_vecs[NUM_VECS_PER_THREAD];
        // Loop 3
        #pragma unroll
        for (int j = 0; j < NUM_VECS_PER_THREAD; j++) {
            // Load K to `k_vecs` ...
        }
        float qk = scale * Qk_dot<scalar_t, THREAD_GROUP_SIZE>::dot(
                        q_vecs[thread_group_offset], k_vecs);
        // Add the ALiBi bias if slopes are given.
        qk += (alibi_slope != 0) ? alibi_slope * (token_idx - seq_len + 1) : 0;
        if (thread_group_offset == 0) {
            // Store the partial reductions to shared memory.
            // Mask
            // Update the max value.
        }
    }
}

先说第一个循环, 其中比较重要的几个参数定义如下:

// [start_block_idx, end_block_idx) is the range of blocks to process.
const int start_block_idx =
    USE_PARTITIONING ? partition_idx * num_blocks_per_partition : 0;
// If not using partitioning, `end_block_idx` should be equal to `num_seq_blocks`.
const int end_block_idx =
    MIN(start_block_idx + num_blocks_per_partition, num_seq_blocks);
// Number of blocks to process.
const int num_blocks = end_block_idx - start_block_idx;

用文字描述就是:

blk_idx 表示当前 thread 所在 warp 需要处理的 PA block 的在 block_table 中索引 (逻辑上的索引).
start_block_idx 和 end_block_idx 表示当前 cuda block 需要处理的 block 范围.
num_blocks 表示当前 cuda block 需要处理的 block 数量.
NUM_WARPS 表示当前 cuda block 中 warp 的数量. 一个 warp 包含 32 个 thread.
warp_idx 表示当前 warp 在当前 cuda block 中的索引.

说人话就是每个 warp 处理一个 PA block, 一开始 cuda block 中的所有 warp 紧密地指向最前面的 NUM_WARPS 个 PA block, 每次循环所有 warp 向后偏移 NUM_WARPS 个 PA block 的长度. 参考下图:

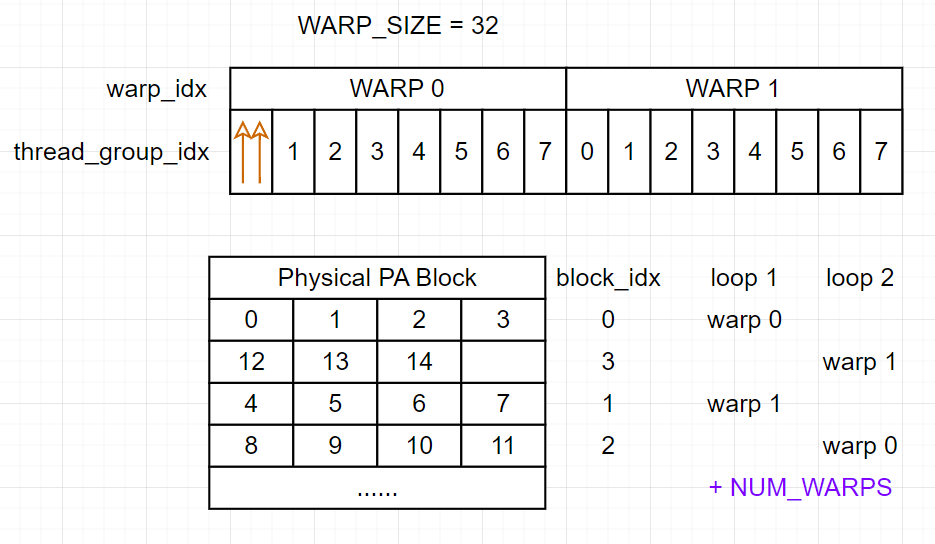
🔔 这里再回顾一下, 一个 PA block 里存放了 BLOCK_SIZE 个 token 的 K 或 V cache.

所以说这个循环和上面读取 Q 的循环一个尿性🤮, 不过是以 warp 的粒度处理数据;

进入了第一个循环内部, 第一步当然是计算当前 thread 对应的 warp 应该计算哪个 PA block (物理上的索引), 因此得到了 physical_block_number:

const int64_t physical_block_number =
    static_cast<int64_t>(block_table[block_idx]);

然后解释第二个循环, 第二个循环的整体目标就是让当前 warp 计算好自己负责的 PA block 中 BLOCK_SIZE 个 token 的 QK 乘积.

先看一下 i 的上界:

constexpr int NUM_TOKENS_PER_THREAD_GROUP =
    DIVIDE_ROUND_UP(BLOCK_SIZE, WARP_SIZE);
// ...

// Loop 1
for (int block_idx = start_block_idx + warp_idx; block_idx < end_block_idx;
        block_idx += NUM_WARPS) {
    // Loop 2
    for (int i = 0; i < NUM_TOKENS_PER_THREAD_GROUP; i++) {
        // ...
    }
    // ...
}

从 kernel 角度看, 每个 thread 需要辅助当前 warp 计算自己负责的一整个 PA block (包含 BLOCK_SIZE 个 token), 而我们把这个过程拆分为 Loop 2 中的 NUM_TOKEN_PER_THREAD_GROUP (也就是 ceil(BLOCK_SIZE / 32)) 次循环;

说人话就是一个 thread group 对应一个 token 中的一个 head, 如果 BLOCK SIZE 太大了后面每个 thread 向后偏移 i * WARP_SIZE 个 token 继续狠狠算🤣.

也因此第二个循环内部一上来先计算了几个偏移量, 并且申请了 thread 内部私有的 k_vecs 数组:

const int physical_block_offset = (thread_group_idx + i * WARP_SIZE) % BLOCK_SIZE;
const int token_idx = block_idx * BLOCK_SIZE + physical_block_offset;
K_vec k_vecs[NUM_VECS_PER_THREAD];

thread_group_idx 表示当前 thread group 在整个 cuda block 中的索引.
☢️ 一个 thread group 在一次循环中负责 fetch 一个 PA block 中 K cache 的一个 token 中自己负责的 head.
☢️ 一个 thread group 负责计算一个 qk 值; 这个值显然是由一个 Q head 和一个 K head 点积得到的.
physical_block_offset 表示当前要算的 token 在当前 PA block 中的偏移量 (注意和前面的 physical_block_number 区分).
加 i * WARP_SIZE 的原因是如果 BLOCK_SIZE 大于 32, 那么一个 warp 要多次循环才能处理完一个 PA block 中的所有 token, 对应 thread_group_idx 需要做偏移.
token_idx 表示当前要算的 token 在整个 seq 的 KV cache 中的索引.
k_vecs 中能存放 NUM_VECS_PER_THREAD 个 VEC, 而一整个 thread group 中所有的 thread 的 k_vecs 合起来才能组成一个 K 的 head (推导参考上面 Q 的 😇). 这就是为什么后面算 QK 的时候要 reduce.

🤔 看到这里读者可能有一个问题: 一个 token 的 K cache 应该对应多个 head, 为什么上面说一个 thread group 只负责一个 head?
答: 因为实际计算的时候, 一个 cuda block 只负责计算一个 head, 对应到 K Cache 乃至后面 V Cache 的位置也是一样的.

这里额外说一下, 读 K 的 head 的一个目标应该是在尽量少的 register 中装下一个 head 的所有元素, 这样后续和 shared memory 中的 Q 做点乘并规约的速度更快. 假设一个 head 有 128 个 float16, 则占用 256B, 而 A100 中一个 thread 最多能有 255 个 32-bit register (也就是 1020B), 此时可以认为一个 thread 能装下一个 head 的所有元素.
但是由于目前 PA kernel 在 BLOCK_SIZE 为 16 的情况下 THREAD_GROUP_SIZE 等于 2, 因此一个 thread 只会装一个 head 的一半元素, 这样可能会导致 register 的使用率不高.

接着进入第三个循环, 目的是让 thread group 从 K cache 中读一个 head, 并存入 k_vecs 中:

// x == THREAD_GROUP_SIZE * VEC_SIZE
// Each thread group fetches x elements from the key at a time.
constexpr int x = 16 / sizeof(cache_t);
//...
// Loop 1
for (int block_idx = start_block_idx + warp_idx; block_idx < end_block_idx;
        block_idx += NUM_WARPS) {
    // Loop 2
    for (int i = 0; i < NUM_TOKENS_PER_THREAD_GROUP; i++) {
        K_vec k_vecs[NUM_VECS_PER_THREAD];
        // Loop 3
        for (int j = 0; j < NUM_VECS_PER_THREAD; j++) {
            const cache_t* k_ptr =
                k_cache + physical_block_number * kv_block_stride +
                kv_head_idx * kv_head_stride + physical_block_offset * x;
            const int vec_idx = thread_group_offset + j * THREAD_GROUP_SIZE;
            const int offset1 = (vec_idx * VEC_SIZE) / x;
            const int offset2 = (vec_idx * VEC_SIZE) % x;
            // if Fp8KVCacheDataType::kAuto
            k_vecs[j] = *reinterpret_cast<const K_vec*>(
              k_ptr + offset1 * BLOCK_SIZE * x + offset2);
        }
        // ...
    }
    // ...
}

老规矩, 先看 j, 本质就是从 0 迭代到 NUM_VECS_PER_THREAD, 每次迭代当前 thread 读取一个 VEC 存入 k_vecs 中.

🔔 回顾:
NUM_VECS_PER_THREAD 表示一个 head 被分成多少个 16B.
k_cache 的 shape 为 (num_blocks, num_kv_heads, head_size/x, block_size, x).

其中的 x 表示一个 thread group 需要读取的元素数量 (VEC_SIZE * THREAD_GROUP_SIZE); 因此作者将 K Cache 的 layout 的最后一维设置为 x 其实也是方便后续 thread group 对 K cache 的读取.

下图具体展示了寻址的过程:

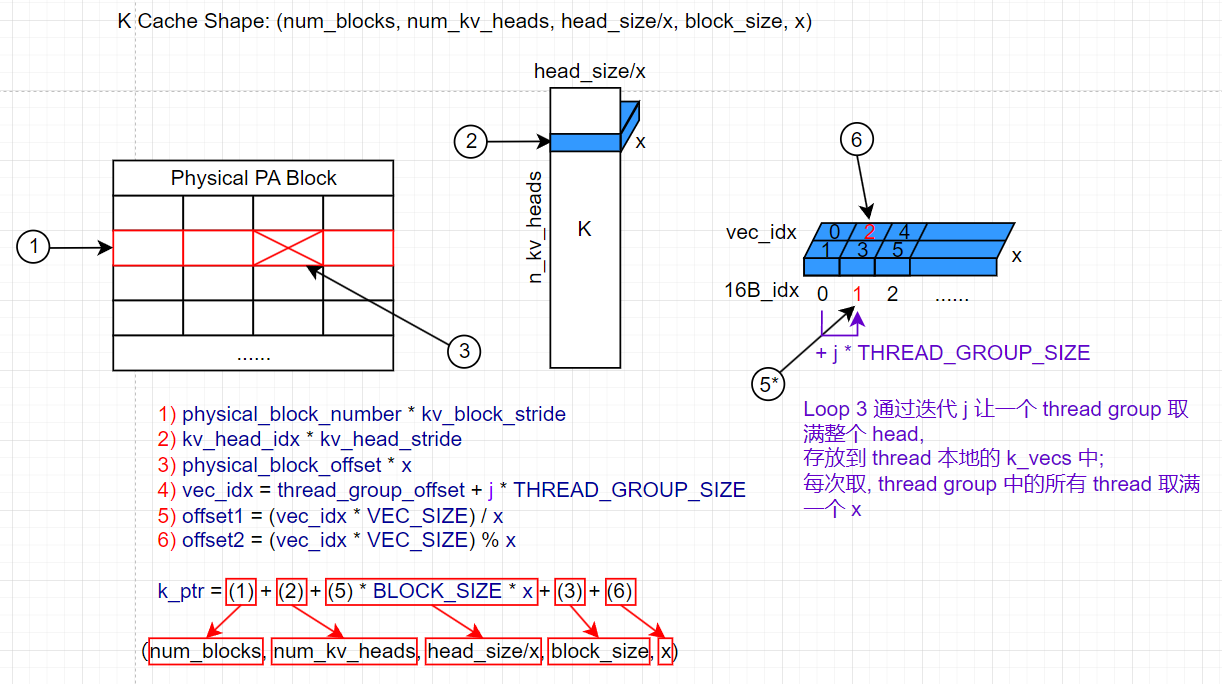
其中:

在 MHSA 中, num_kv_heads 等于 num_heads; 而在 GQA, MQA 中, num_kv_heads 小于 num_heads.
(1) 负责找到当前 thread 属于的 warp 要处理哪个 PA block.
(2) 负责找到当前 thread 要计算的 head 在 K cache 中的位置. 这个 head 的索引和 Q 中 head 的索引在 MHSA 中相同.
(3) 负责找到当前 thread group 要计算的 token 在当前 PA block 中的位置.
(5) 负责找到当前 thread 在需要读取的 head (蓝色长方体) 中 x 的偏移, 通过 j 进行迭代读取. 每次循环 thread group 中的所有 thread 取一个 x.
(6) 负责找到当前 thread 在 thread gruop 中读取的 x 中 VEC 的偏移; thread 一次读取一个 VEC.

🤔 为什么 (5) 在实际寻址时需要 * BLOCK_SIZE * x ?
答: 这是根据 k_cache 的 layout 得到的 stride. 同理 (3) * x 也是 stride.

第 3 个循环结束时当前 warp 负责的每个 token 中需要的 K cache head 已经全被加载入 thread 本地的 k_vecs 中了.

由于一个 thread group 的 k_vecs 才能真正组成一个 head, 在退回第二个循环进行 QK dot 的时候, 需要做个 reduction, 具体的范围就是 THREAD_GROUP_SIZE 个 thread:

// Loop 1
for (int block_idx = start_block_idx + warp_idx; block_idx < end_block_idx;
        block_idx += NUM_WARPS) {
    // Loop 2
    for (int i = 0; i < NUM_TOKENS_PER_THREAD_GROUP; i++) {
        K_vec k_vecs[NUM_VECS_PER_THREAD];
        // Loop 3
        for (int j = 0; j < NUM_VECS_PER_THREAD; j++) {
            // ...
        }
        float qk = scale * Qk_dot<scalar_t, THREAD_GROUP_SIZE>::dot(
                             q_vecs[thread_group_offset], k_vecs);
    }
    // ...
}

计算完 qk 后, 由当前 thread group 中第一个 (offset 为 0) 的 thread 对自己刚才算出来的 qk 进行 mask, 顺便看看如果没有 mask 掉, 把 qk_max 赋值为 qk:

if (thread_group_offset == 0) {
    // Store the partial reductions to shared memory.
    // NOTE(woosuk): It is required to zero out the masked logits.
    const bool mask = token_idx >= seq_len;
    logits[token_idx - start_token_idx] = mask ? 0.f : qk;
    // Update the max value.
    qk_max = mask ? qk_max : fmaxf(qk_max, qk);
}

🧐 为什么要做 mask?

因为一个 seq 的最后一个 PA block 可能覆盖不满 BLOCK_SIZE 个 token. 这里的 mask 就是把那部分 qk 置零.

5.4. Softmax

我勒个 QK 啊, 总算算完了, 锐克 five 都要被抽清仓了. 页意丁真, 鉴定为开算 softmax.

主要步骤就是广播然后算, 算 softmax 需要知道每个 head 对应的 qk 的最大值. 由于一个 cuda block 负责的就是一个 head, 对于这个 head 上面的计算步骤一共算了 cache_len个 token 的 qk, 因此需要做一个 cuda block 范围的规约, 找到其中最大的 qk 值.

先在 warp 层面规约.

__shared__ float red_smem[2 * NUM_WARPS];

// ...

// Perform reduction across the threads in the same warp to get the
// max qk value for each "warp" (not across the thread block yet).
// The 0-th thread of each thread group already has its max qk value.
#pragma unroll
for (int mask = WARP_SIZE / 2; mask >= THREAD_GROUP_SIZE; mask /= 2) {
    qk_max = fmaxf(qk_max, VLLM_SHFL_XOR_SYNC(qk_max, mask));
}
if (lane == 0) {
    red_smem[warp_idx] = qk_max;
}
__syncthreads();

red_smem 是之前申请的 shared memory.
VLLM_SHFL_XOR_SYNC 是一个 warp 内的 shuffle 操作, 具体来说, 在每次循环时, 每个 thread 和自己相距 mask 位置的线程交换数据 (交换来的数据通过 fmaxf 比较), 并且 mask 会逐渐减半, 直到 THREAD_GROUP_SIZE 为止.
lane 表示当前 warp 中的线程索引.

接着再对每个 warp 的最大值进行规约, 由于每个 warp 的最大值都被存入了 red_smem 中, 所以只需要再次进行 shuffle 操作即可.

// TODO(woosuk): Refactor this part.
// Get the max qk value for the sequence.
qk_max = lane < NUM_WARPS ? red_smem[lane] : -FLT_MAX;
#pragma unroll
for (int mask = NUM_WARPS / 2; mask >= 1; mask /= 2) {
    qk_max = fmaxf(qk_max, VLLM_SHFL_XOR_SYNC(qk_max, mask));
}

此时, 第 1 个线程的 qk_max 就是当前 cuda block 中所有 warp 中最大的 qk 值. 将其广播给所有线程:

// Broadcast the max qk value to all threads.
qk_max = VLLM_SHFL_SYNC(qk_max, 0);

在获得了 qk_max 后, 就可以计算 softmax 了:

// Get the sum of the exp values.
float exp_sum = 0.f;
for (int i = thread_idx; i < num_tokens; i += NUM_THREADS) {
    float val = __expf(logits[i] - qk_max);
    logits[i] = val;
    exp_sum += val;
}
exp_sum = block_sum<NUM_WARPS>(&red_smem[NUM_WARPS], exp_sum);

// Compute softmax.
const float inv_sum = __fdividef(1.f, exp_sum + 1e-6f);
for (int i = thread_idx; i < num_tokens; i += NUM_THREADS) {
    logits[i] *= inv_sum;
}
__syncthreads();

5.5. LV (Logits * Value)

上图展示了 LV 的计算过程, 主要区别是由于要计算 Logits 的 shape 可以表示为 (num_heads, num_seqs, cache_len), 而 V 的 shape 可以表示为 (num_heads, cache_len, head_size), 因此 LV 的矩阵乘法中, 每计算一个元素需要读取 logits 的一行和 V 的一列进行计算.

此时, 一个 cuda block 的职责从 “自 Q 中读取一个 head” 转变为 “计算 output 中的一个 head”.

🧐 为什么在计算 LV 时, 去掉了 thread group 的概念, 每个 thread 都被设定为每次读取 16B?

因为现在每计算一个元素, 需要的访存量更大, 因此给每个 thread 分配了更多的数据读取量. 也就是说, V_VEC_SIZE 比 VEC_SIZE 更大.

由于 cuda 访存模式按行读取更快, 所以实际的计算结果在遍历 PA block 时线程内部利用 accs 进行累计 (以实现与 V 的一列进行计算的行为):

constexpr int NUM_V_VECS_PER_ROW = BLOCK_SIZE / V_VEC_SIZE;
constexpr int NUM_ROWS_PER_ITER = WARP_SIZE / NUM_V_VECS_PER_ROW;
constexpr int NUM_ROWS_PER_THREAD =
    DIVIDE_ROUND_UP(HEAD_SIZE, NUM_ROWS_PER_ITER);

// NOTE(woosuk): We use FP32 for the accumulator for better accuracy.
float accs[NUM_ROWS_PER_THREAD];

for (int block_idx = start_block_idx + warp_idx; block_idx < end_block_idx;
        block_idx += NUM_WARPS) {
    V_vec v_vec;
    // ...
    for (int i = 0; i < NUM_ROWS_PER_THREAD; i++) {
        // ...
        for (int j = 0; j < V_VEC_SIZE; j++) {
            // Load V to `v_vec` ...
            v_vec_ptr[j] = token_idx + j < seq_len ? v_vec_ptr[j] : zero_value;
        }
        // Accumulate the dot product.
        accs[i] += dot(logits_vec, v_vec);
    }
}

由于每个线程负责的累计部分不满一整行/列, 所以进行规约:

// Perform reduction within each warp.
#pragma unroll
  for (int i = 0; i < NUM_ROWS_PER_THREAD; i++) {
    float acc = accs[i];
#pragma unroll
    for (int mask = NUM_V_VECS_PER_ROW / 2; mask >= 1; mask /= 2) {
      acc += VLLM_SHFL_XOR_SYNC(acc, mask);
    }
    accs[i] = acc;
  }

  // NOTE(woosuk): A barrier is required because the shared memory space for
  // logits is reused for the output.
  __syncthreads();

  // Perform reduction across warps.
  float* out_smem = reinterpret_cast<float*>(shared_mem);
#pragma unroll
  for (int i = NUM_WARPS; i > 1; i /= 2) {
    int mid = i / 2;
    // Upper warps write to shared memory.
    if (warp_idx >= mid && warp_idx < i) {
      float* dst = &out_smem[(warp_idx - mid) * HEAD_SIZE];
#pragma unroll
      for (int i = 0; i < NUM_ROWS_PER_THREAD; i++) {
        const int row_idx = lane / NUM_V_VECS_PER_ROW + i * NUM_ROWS_PER_ITER;
        if (row_idx < HEAD_SIZE && lane % NUM_V_VECS_PER_ROW == 0) {
          dst[row_idx] = accs[i];
        }
      }
    }
    __syncthreads();

    // Lower warps update the output.
    if (warp_idx < mid) {
      const float* src = &out_smem[warp_idx * HEAD_SIZE];
#pragma unroll
      for (int i = 0; i < NUM_ROWS_PER_THREAD; i++) {
        const int row_idx = lane / NUM_V_VECS_PER_ROW + i * NUM_ROWS_PER_ITER;
        if (row_idx < HEAD_SIZE && lane % NUM_V_VECS_PER_ROW == 0) {
          accs[i] += src[row_idx];
        }
      }
    }
    __syncthreads();
  }

最后写入到输出中:

  // Write the final output.
  if (warp_idx == 0) {
    scalar_t* out_ptr =
        out + seq_idx * num_heads * max_num_partitions * HEAD_SIZE +
        head_idx * max_num_partitions * HEAD_SIZE + partition_idx * HEAD_SIZE;
#pragma unroll
    for (int i = 0; i < NUM_ROWS_PER_THREAD; i++) {
      const int row_idx = lane / NUM_V_VECS_PER_ROW + i * NUM_ROWS_PER_ITER;
      if (row_idx < HEAD_SIZE && lane % NUM_V_VECS_PER_ROW == 0) {
        from_float(*(out_ptr + row_idx), accs[i]);
      }
    }
  }

1. Why Attention’s $O_i$ only depends on $Q_i$#

2. KV Cache Incremental Process#

2.1. Prefilling: Initial Input (Complete Sequence) Calculation#

2.2. Decoding: Incremental Calculation When Predicting Next Token:#

3. Paged Attention in vllm#

3.1. Motivation: Memory Wastes#

3.2. Solution: Managing Caches with Pages#

5. Paged Attention Kernel in Details#

5.1. 输入输出输出分析和参数说明#

5.2.Shared Memory: q_vecs 的写入#

5.3. 读取 K Cache 并计算 QK#

5.4. Softmax#

5.5. LV (Logits * Value)#