Reference: The Deep Learning Compiler: A Comprehensive Survey
1. ABSTRACT
The DL compilers take the DL models described in different DL frameworks as input, and then generate optimized codes for diverse DL hardware as output.
Generally, the DL hardware can be divided into the following categories:
- General-purpose hardware with software-hardware co-design;
- Dedicated hardware fully customized for DL models;
- Neuromorphic hardware inspired by biological brain science.
However, the drawback of relying on the libraries is that they usually fall behind the rapid development of DL models, and thus fail to utilize the DL chips efficiently.
To address the drawback of DL libraries and tools, as well as alleviate the burden of optimizing the DL models on each DL hardware manually, the DL community has resorted to the domain specific compilers for rescue.
The DL compilers take the model definitions described in the DL frameworks as inputs, and generate efficient code implementations on various DL hardware as outputs.
2. BACKGROUND
2.1. Deep Learning Frameworks
…
2.3. Hardware-specific DL Code Generator
Field Programmable Gate Arrays (FPGAs) are reprogrammable integrated circuits that contain an array of programmable logic blocks. Programmers can configure them after manufacturing.
The FPGA can bridge the gap between CPUs/GPUs and ASICs, which causes the FPGA to be an attractive platform for deep learning.
Mapping DL models to FPGAs remains a complicated work even with HLS, because:
- DL models are usually described by the languages of DL frameworks rather than bare mental C/C++ code;
- DL-specific information and optimizations are hard to be leveraged.
The hardware-specific code generator targeting FPGA take the DL models or their domain-specific languages (DSLs) as the input, conduct the domain-specific (about FPGA and DL) optimizations and mappings, then generate the HLS or Verilog/VHDL and finally generate the bitstream. They can be classified into two categories according to the generated architectures of FPGA-based accelerators: the processor architecture and the streaming architecture.
The processor architecture has similarities with general-purpose processors. An FPGA accelerator of this architecture usually comprises several Processing Units (PUs), which are comprised of on-chip buffers and multiple smaller Processing Engines (PEs).
The streaming architecture has similarities with pipelines. An FPGA accelerator of this architecture consists of multiple different hardware blocks, and it nearly has one hardware block for each layer of an input DL mode
3. COMMON DESIGN ARCHITECTURE OF DL COMPILERS
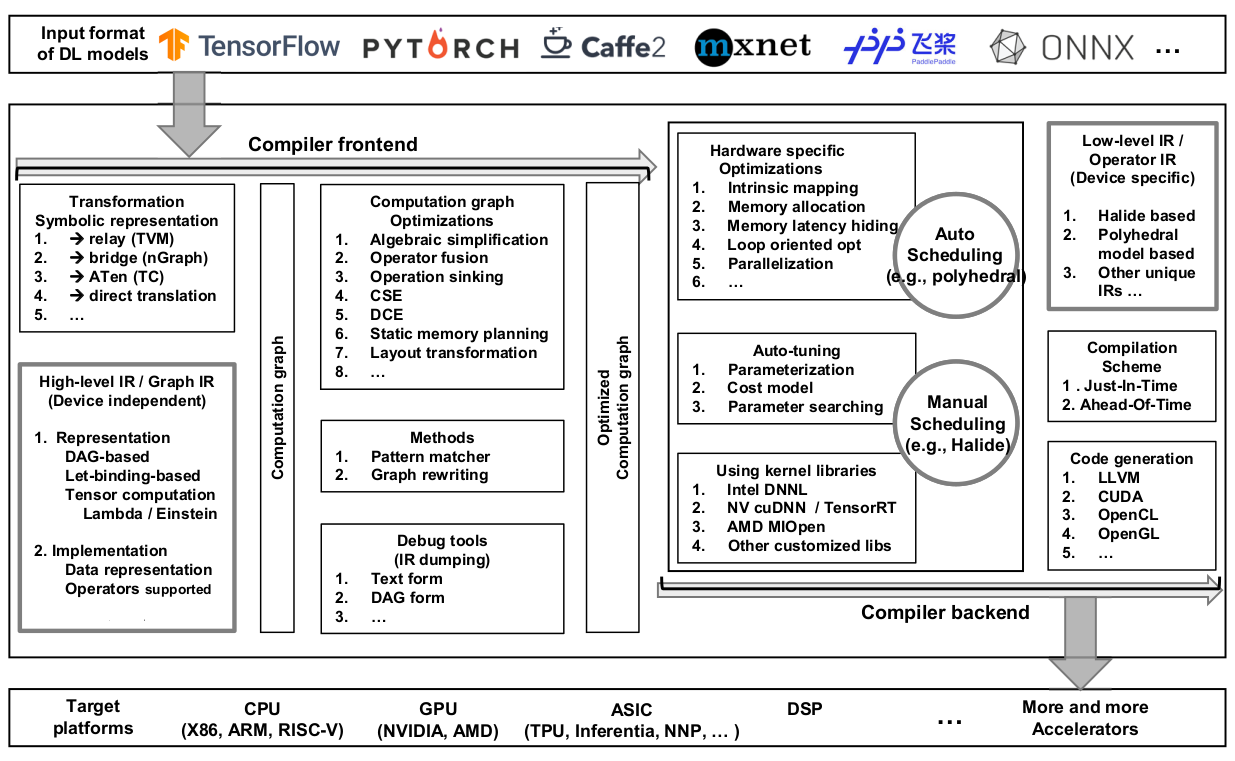
Figure 1. Common Design Architecture of DL Compilers.
4.1. High-level IR
DAG-based IR - DAG-based IR is one of the most traditional ways for the compilers to build a computation graph, with nodes and edges organized as a directed acyclic graph (DAG). In DL compilers, the nodes of a DAG represent the atomic DL operators (convolution, pooling, etc.), and the edges represent the tensors. And the graph is acyclic without loops, which differs from the data dependence graphs (DDG) of generic compilers.
Let-binding-based IR - Let-binding is one method to solve the semantic ambiguity by offering let expression to certain functions with restricted scope used by many high-level programming languages such as Javascript, F#, and Scheme. When using the let keyword to define an expression, a let node is generated, and then it points to the operator and variable in the expression instead of just building computational relation between variables as a DAG.
Representing Tensor Computation - Different graph IRs have different ways to represent the computation on tensors:
- Function Based
- Lambda Based
- Einstein notation
Data representation - The data in DL compilers (e.g., inputs, weights, and intermediate data) are usually organized in the form of tensors, which are also known as multi-dimensional arrays. The DL compilers can represent tensor data directly by memory pointers, or in a more flexible way by placeholders. A placeholder contains the size for each dimension of a tensor. Alternatively, the dimension sizes of the tensor can be marked as unknown. For optimizations, the DL compilers require the data layout information. In addition, the bound of iterators should be inferred according to the placeholders.
4.2. Low-level IR
Low-level IR describes the computation of a DL model in a more fine-grained representation than that in high-level IR, which enables the target-dependent optimizations by providing interfaces to tune the computation and memory access.
Halide-based IR - Halide is firstly proposed to parallelize image processing, and it is proven to be extensible and efficient in DL compilers (e.g., TVM). The fundamental philosophy of Halide is the separation of computation and schedule.
Polyhedral-based IR - The polyhedral model is an important technique adopted in DL compilers. It uses linear programming, affine transformations, and other mathematical methods to optimize loop-based codes with static control flow of bounds and branches.
4.3. Frontend Optimizations
After constructing the computation graph, the frontend applies graph-level optimizations.
The frontend optimizations are usually defined by passes, and can be applied by traversing the nodes of the computation graph and performing the graph transformations:
- Capture the specific features from the computation graph;
- Rewrite the graph for optimization.
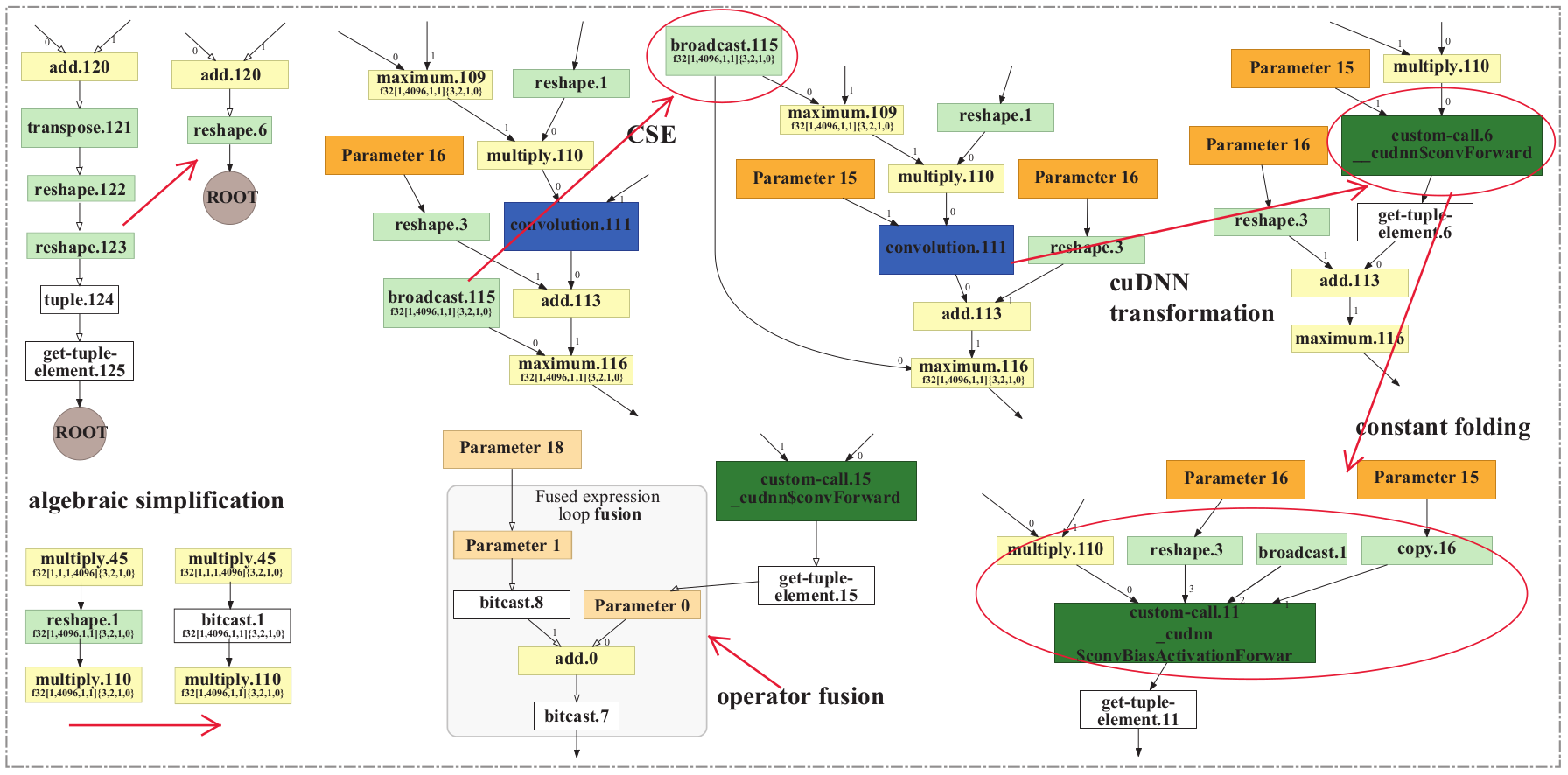
Figure 2. Example of computation graph optimizations, taken from the HLO graph of AlexNet on Volta GPU using TensorFlow XLA.
4.3.1. Node-level optimizations
The nodes of the computation graph are coarse enough to enable optimizations inside a single node. And the node-level optimizations include node elimination that eliminates unnecessary nodes and node replacement that replaces nodes with other lower-cost nodes.
4.3.2. Block-level optimizations
Algebraic simplification
The algebraic simplification opti- mizations consist of :
- algebraic identification;
- strength reduction, with which we can replace more expensive operators by cheaper ones;
- constant folding, with which we can replace the constant expressions by their values.
Such optimizations consider a sequence of nodes, then take advantage of commutativity, associativity, and distributivity of different kinds of nodes to simplify the computation.
Operator fusion
Operator fusion is indispensable optimization of DL compilers. It enables better sharing of computation, eliminates intermediate allocations, facilitates further optimization by combining loop nests, as well as reduces launch and synchronization overhead.
Operator sinking
This optimization sinks the operations such as transposes below operations such as batch normalization, ReLU, sigmoid, and channel shuffle. By this optimization, many similar operations are moved closer to each other, creating more opportunities for algebraic simplification.
4.3.3. Dataflow-level optimizations
- Common sub-expression elimination (CSE)
- Dead code elimination (DCE)
- Static memory planning - Static memory planning optimizations are performed to reuse the memory buffers as much as possible. Usually, there are two approaches: in-place memory sharing and standard memory sharing.
- Layout transformation - Layout transformation tries to find the best data layouts to store tensors in the computation graph and then inserts the layout transformation nodes to the graph.
4.4. Backend Optimizations
The backends of DL compilers have commonly included various hardware-specific optimizations, auto-tuning techniques, and optimized kernel libraries. Hardware-specific optimizations enable efficient code generation for different hardware targets. Whereas, auto-tuning has been essential in the compiler backend to alleviate the manual efforts to derive the optimal parameter configurations. Besides, highly-optimized kernel libraries are also widely used on general-purpose processors and other customized DL accelerators.
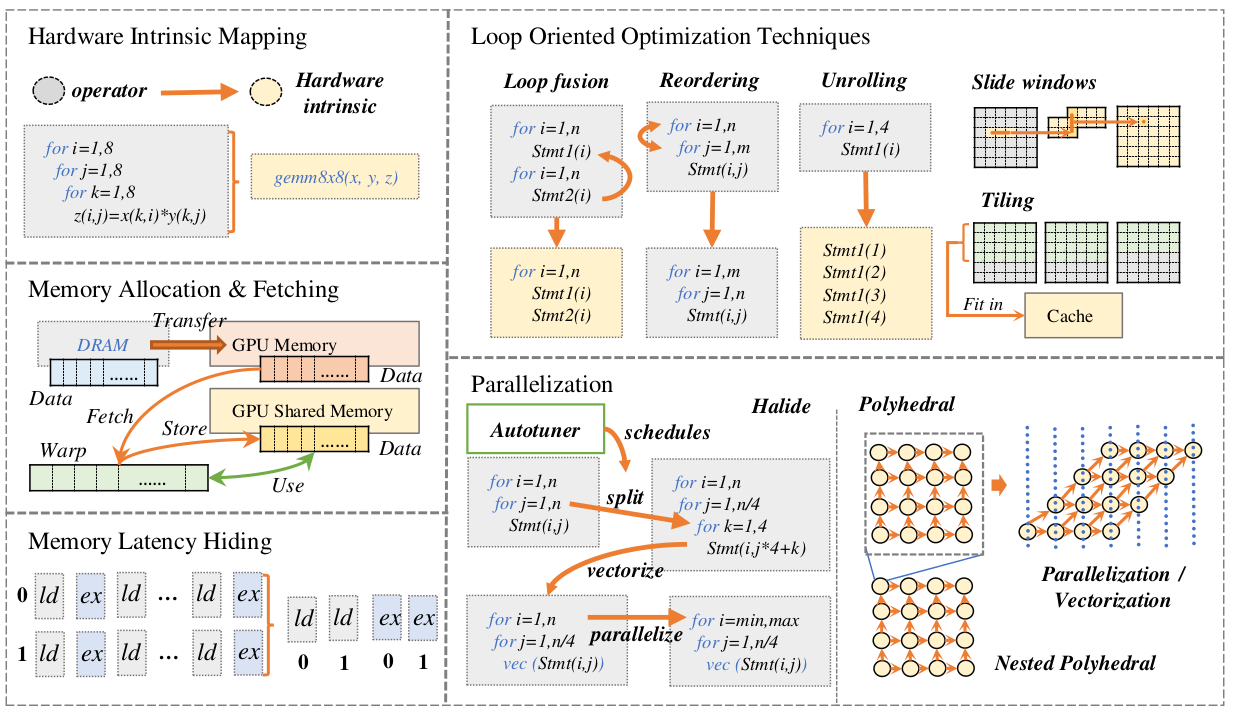
Figure 3. Overview of hardware-specific optimizations applied in DL compilers.
5. FUTURE DIRECTIONS
- Dynamic shape and pre/post processing
- Advanced auto-tuning
- Polyhedral model
- Subgraph partitioning
- Quantization
- Unified optimizations
- Differentiable programming
- Privacy protection
- Training support